Branch Channel Attention
different branches
SKNet
文章标题:Selective Kernel Networks 作者:Xiang Li, Wenhai Wang, Xiaolin Hu, Jian Yang 发表时间:(CVPR 2019)
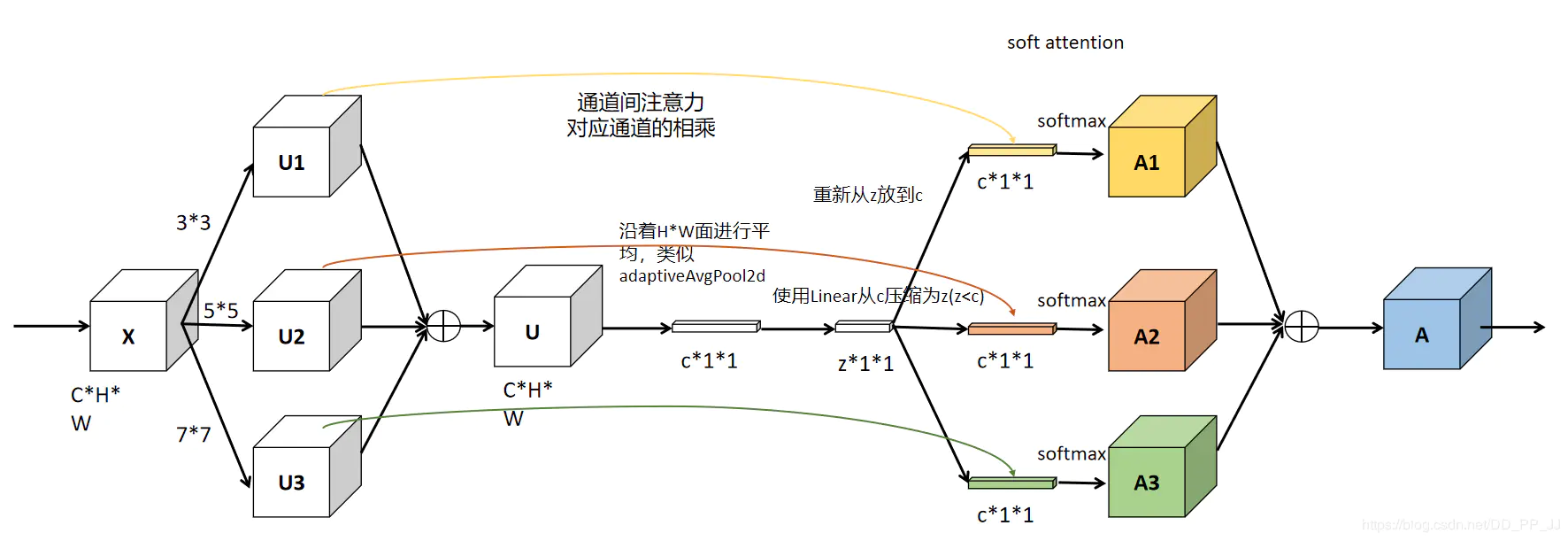
用multiple scale feature汇总的information来channel-wise地指导如何分配侧重使用哪个kernel的表征
一种非线性方法来聚合来自多个内核的信息,以实现神经元的自适应感受野大小
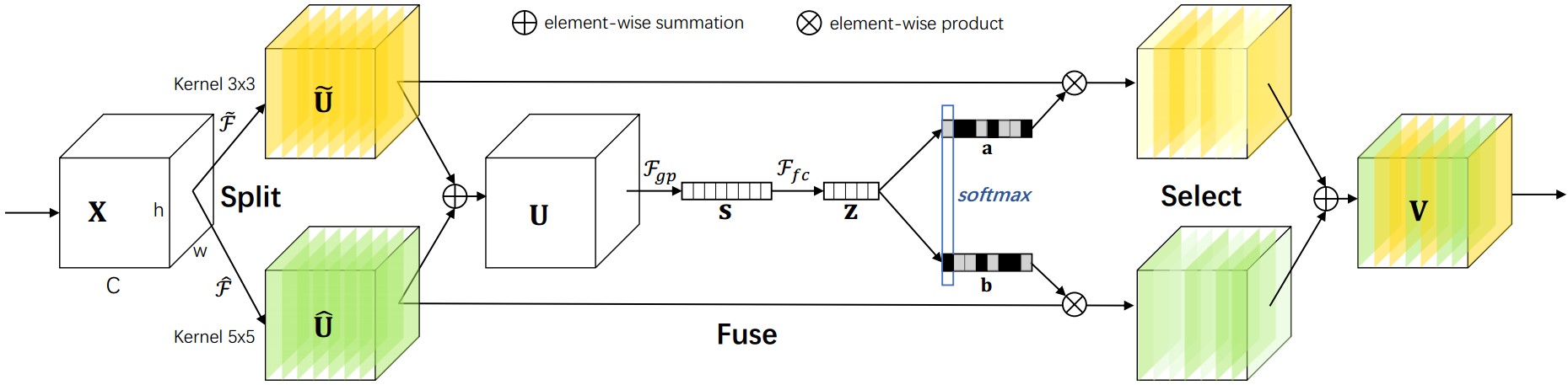
$$ U=\tilde U+\hat U\\ s_c=F_{gp}(U_c)=\frac{1}{H\times W}\sum_{i=1}^H\sum_{j=1}^WU_c(i,j)\\ z=F_{fc}(s)=\delta(B(Ws)) 降维处理\\ $$Split:生成具有不同内核大小的多条路径,这些路径对应于不同感受野(RF,receptive field) 大小的神经元
$X\in R^{H’\times W’\times C’} $
$\tilde F:X\to \tilde U \in R^{H\times W\times C} $ kernel size $3\times3$
$\hat F:X\to \hat U \in R^{H\times W\times C}$ kernel size $5\times5$:使用空洞卷积$3\times3$,空洞系数为2。
Fuse:聚合来自多个路径的信息,以获得选择权重的全局和综合表示。
$$ V_c=a_c\cdot\tilde U_c + b_c\cdot \hat U_c\\\ a_c+b_c=1\\ V_c\in R^{H\times W} $$$s\in R^c$;$\delta$:ReLU;$z\in R^{d\times1}$;$W\in R^{d\times C}$:批量归一化;
$d=max(C/r,L)$ L:d的最小值,本文设置32
Select:根据选择权重聚合不同大小内核的特征图
$$ a_c=\frac{e^{A_cz}}{e^{A_cz}+e^{B_cz}}\\ b_c=\frac{e^{B_cz}}{e^{A_cz}+e^{B_cz}}\\ $$$ A,B ∈R^{C\times d}$ ,$ a,b$ 分别表示 $\tilde U,\hat U$的软注意力向量。$A_c ∈ R^{1\times d }$是 A 的第$ c $行,$a_c$ 是 a 的第 $c $个元素,同理$B_c,b_c$。
$$ U_k=F_k(X) \\ U = \sum_{k=1}^K U_k \\ z = \delta(BN(WGAP(U))) \\ s_k^{(c)} = \frac{e^{W_k^{(c)}z}}{\sum_{k=1}^K e^{W_k^{(c)}z}} \\ Y=\sum_{k=1}^K s_kU_k \\ global\ average\ pooling\rightarrow MLP\rightarrow softmax $$$SK[M,G,r]\to SK[2,32,16]$
M:确定要聚合的不同内核的选择数量
G:控制每条路径的基数的组号
r:reduction ratio
| |
different conv kernels
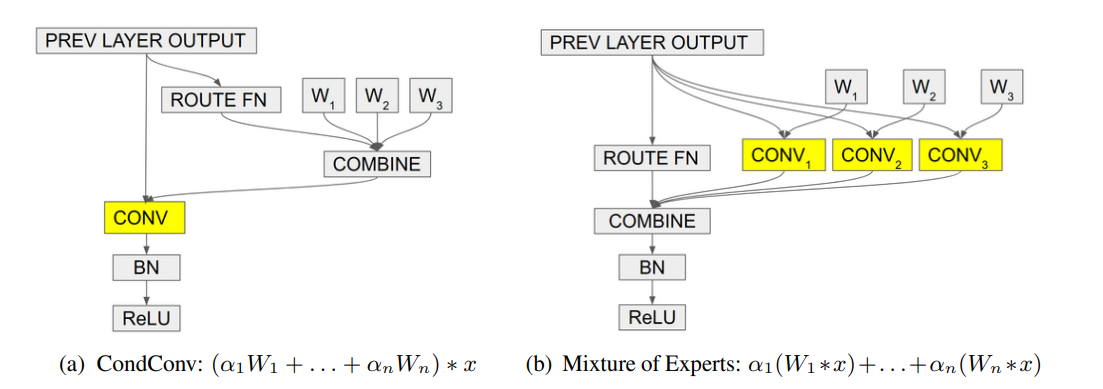
CondConv
文章标题:CondConv: Conditionally Parameterized Convolutions for Efficient Inference 作者:Brandon Yang, Gabriel Bender, Quoc V. Le, Jiquan Ngiam 发表时间:(NIPS 2019)
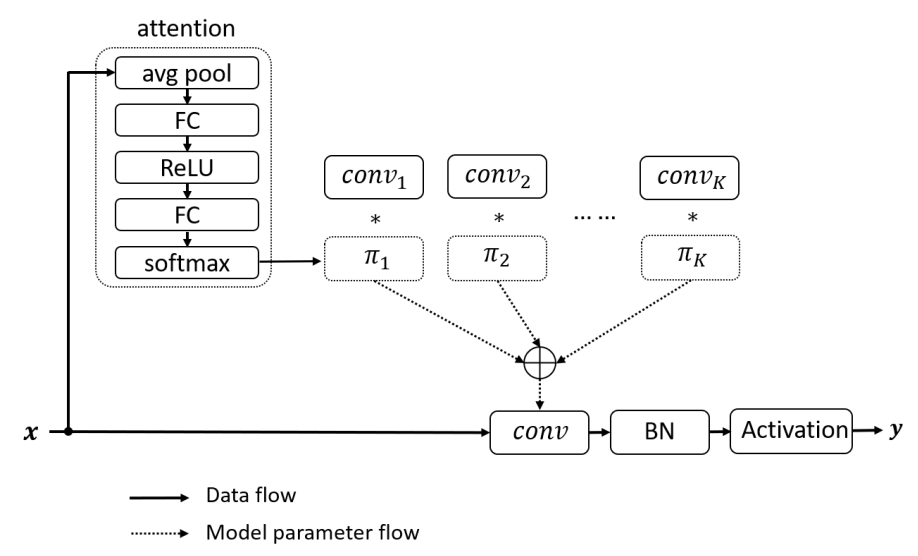
DynamicConv
文章标题:Dynamic Convolution: Attention over Convolution Kernels 作者:Yinpeng Chen, Xiyang Dai, Mengchen Liu, Dongdong Chen, Lu Yuan, Zicheng Liu 发表时间:(CVPR 2020)