GAN
GAN
文章标题:Generative Adversarial Networks 作者:Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair,
Aaron Courville, Yoshua Bengio
发表时间:(NIPS 2014)
——Learnable cost function损失函数时从数据学习得到的
——Mini-Max game based on Nash Equilibrium 博弈论
——Hard to training -no guarantee to equilibrium
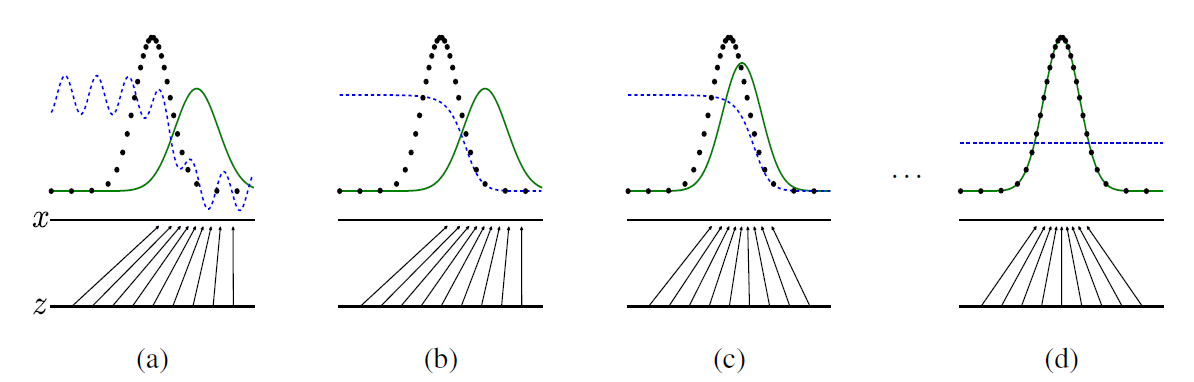
噪音 z 一维标量 (均匀分布采样得来),数据 x 也是 一维标量(图中黑点,高斯分布)。
G对噪声z的映射
D对噪声z的映射到数据空间的判断线
(a):G 把 均匀分布采样得到的噪声 z 映射到 绿色高斯分布
(b):D 尽可能地去学习如何判断
真实数据均值更靠左,将左侧的数据判断为真 1, 将右侧数据判断为假 0
(c):G 尽可能地去糊弄 D,把高斯分布的均值中心往左挪动
(d):G 把 来自均匀分布的噪声,映射成和真实 data x 相似的高斯分布。D 对来自真实采样的数据 or G 生成的数据无法判断来源,概率都是 0.5
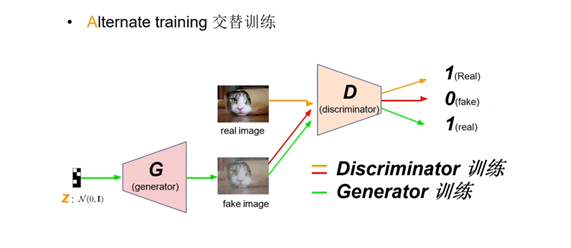
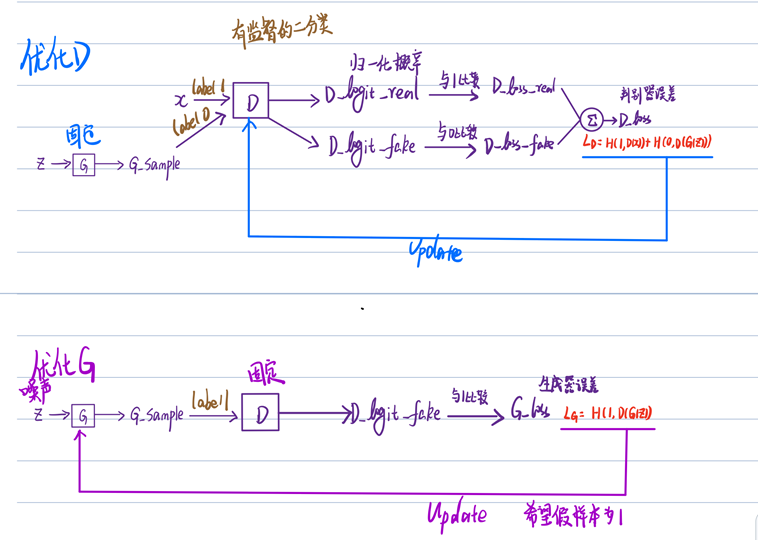
Step1:Fix generator G , and update discriminator D.
训练D:D learns to assign high scores to real objects and low scores to generated objects.(提高判断力,分辨真假,生成数据为假)
Step2:Fix discriminator D, and update generator G .
训练G:G learns to“fool”the discriminator.(提高造假能力,改进生成数据,使其接近真实数据)
 |  |
| GAN_Alogorithm | 流程 |
k 不能太小 –> 保证 判别器 D 有足够的更新
k 不能太大 –> D 过于完美,$D(G(z^{x(i)}) = 0$,对值为 0 求导,G 梯度更新有困难
k 的设计目标:使得 D 和 G 的更新进度差不多
全局最优解证明
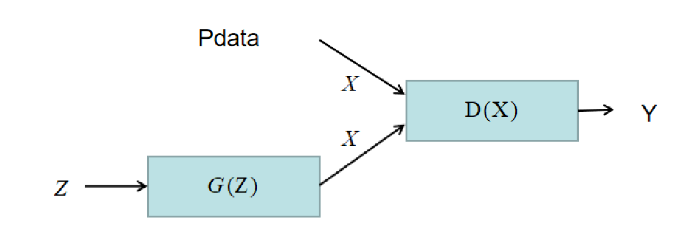
$P_{data}$:${x_i}_{i=1}^N$
$P_g(x;\theta_g)$:generator,$G(z;\theta_g)$
$y|x$:discriminater,$P(y=1|x)=D(x)$,$P(y=0|x)=1-D(x)$
$$ \begin{equation} V(D,G) = \mathbb{E}_{x\sim P_{data}}[\log D(x)] + \mathbb{E}_{x\sim P_{z}}[\log (1-D(G(z)))] \end{equation} $$$$ \begin{equation} \theta_g = \arg\max_{\theta_g} \sum_{i=1}^N \log P_g(x_i) \end{equation} $$$$ \arg\min_{\theta_g} \text{KL}(P_{data}\|P_g) $$$$ \begin{equation} \begin{split} \max_D V(D,G) = & \int P_{\text{data}} \log D dx + \int P_g \log(1-D) dx \\ =& \int (P_{\text{data}} \log D + P_g \log(1-D)) dx \end{split} \end{equation} $$$$ \begin{equation} \begin{split} \frac{\partial \max_D V(D,G)}{\partial D} = & \frac{\partial}{\partial D} \int \left[ P_{\text{data}} \log D + P_g \log(1-D) \right]dx \\ = & \int \frac{\partial}{\partial D} \left[ P_{\text{data}} \log D + P_g \log(1-D) \right]dx \\ = & \int P_{\text{data} }\cdot \frac{1}{D} + P_g \frac{-1}{1-D} dx \\ = & 0 \\ \end{split} \end{equation} $$$$ \begin{equation} D_G^\ast = \frac{P_{\text{data}}}{P_{\text{data}} + P_{g}} \end{equation} $$$$ \begin{equation} \begin{split} \min_G \max_D V(D,G) = & \min_G V(D_G^\ast,G) \\ = & \min_G \mathbb{E}_{x\sim P_{\text{data}}} \left[ \log \frac{P_{\text{data}}}{P_{\text{data}} + P_{g}}\right] + \mathbb{E}_{x\sim P_{g}} \left[ \log \frac{P_g}{P_{\text{data}} + P_{g}}\right] \\ = & \min_G \mathbb{E}_{x\sim P_{\text{data}}} \left[ \log \frac{P_{\text{data}}}{\frac{P_{\text{data}} + P_{g}}{2}} \cdot \frac{1}{2}\right] + \mathbb{E}_{x\sim P_{g}} \left[ \log \frac{P_g}{\frac{P_{\text{data}} + P_{g}}{2}} \cdot \frac{1}{2}\right] \\ = & \min_G \text{KL}\left[ P_{\text{data}} \| \frac{P_{\text{data}} + P_{g}}{2} \right] + log\frac{1}{2} +\text{KL}\left[ P_{g} \| \frac{P_{\text{data}} + P_{g}}{2} \right]+ log\frac{1}{2} \\ = & \min_G (-log 4+2\cdot JS(P_{data}||P_g))\\ \geq & - \log 4 \end{split} \end{equation} $$当且仅当$P_{\text{data}} = P_{g} = \frac{P_{\text{data}} + P_{g}}{2}$时,等号成立。此时,$P^\ast_g = P_d,P^\ast_d = \frac{1}{2}$。
KL散度:
$$ KL(P||Q)=\sum P(x) log\frac{P(x)}{Q(x)} or \int P(x) log\frac{P(x)}{Q(x)} dx $$JS散度:
$$ JS(P_1 || P_2)=\frac{1}{2}KL(P_1||\frac{P_1+P_2}{2})+\frac{1}{2}KL(P_2||\frac{P_1+P_2}{2}) $$拓展阅读
趣味demo
交互式可视化GAN Lab:https://poloclub.github.io/ganlab
交互式可视化GAN Lab视频讲解:https://www.bilibili.com/video/BV1R44y1377T
照片转动漫AnimeGAN:https://github.com/TachibanaYoshino/AnimeGAN
英伟达GauGAN2神笔马良:http://gaugan.org/gaugan2/
不存在的人脸:https://thispersondoesnotexist.com/
不存在的花瓶:https://thisvesseldoesnotexist.com
不存在的梗图:https://imgflip.com/ai-meme
黑白老照片上色:https://deepai.org/machine-learning-model/colorizer
黑白老照片上色:https://github.com/jantic/DeOldify
黑白老照片上色:https://www.myheritage.com/incolor
OpenAI DALLE-2:https://openai.com/dall-e-2
B站:【机器学习】白板推导系列(三十一) ~ 生成对抗网络(GAN)
OpenMMLab开源图像生成算法库MMGeneration
An Annotated Proof of Generative Adversarial Networks with Implementation Notes